Introduction

This is the start of probably the most important and difficult unit to master in all of physics. First, introductions: Isaac Newton is a name well known in physics and mathematics for his breakthroughs and innovations in both fields. In this section, we will begin our study of dynamics starting with his three laws of motion. It is good to first define what forces are: a push or pull that may result in motion.

However, you will see later that a force may not necessarily directly cause motion, but rather it directly changes motion, which is an important concept to recognize. The unit of force is the newton, represented by $\textrm N$. This actually a derived unit, with units $\frac{\textrm{kg} \cdot \textrm m}{\textrm{s}^2}$. We will show how this is derived later on. Force is a vector quantity, meaning it has a direction and magnitude. This will become especially important more later on, when we introduce the idea of a free-body diagram.

Newton's First Law

Let’s break this down into pieces. "State of motion" refers to whether an object is moving and how it is moving. So, this law dictates that objects at rest will remain at rest, and objects in motion will remain in motion (in a straight line, since changing direction changes the velocity of an object). However, there is one small quirk that is not mentioned here. This only holds true when the net, total, or sum of all the external forces acting on an object is zero.

Looking at a real world example, the reason we see objects slow down as they move across surfaces is due to the frictional force. A good way to demonstrate this principle is to use a near-frictionless surface like ice. An object set into motion on ice will move in a straight line at basically constant velocity until it hits something. This opposes the commonly perceived idea that force is directly responsible for causing motion, but rather, force changes motion. As seen in the ice example, a continuous force is not required to keep an object moving. This idea is super important and will come up later on.

The resistance an object offers to being set into motion or being set to rest is its inertia, and it is directly proportional to its mass. There is no numerical quantity corresponding to this, but just know that more massive objects have greater inertia. Often times, an object's mass is called its inertial mass.
This law is not used in calculations, but it justifies the entirety of force analysis and gives us an idea as to what forces do.

All these things that Newton stated are only valid in an inertial reference frame. An inertial reference frame is a reference frame, or coordinate system, that which objects obey Newton's First Law. That means the frame itself is not accelerating, because if it was, the objects would accelerate without external forces, and since acceleration is defined as change in velocity, its velocity, or motion, is changing, and that is a violation of Newton's First Law. Furthermore, Newton's First Law does not also hold true for a frame that is constantly changing orientation, the more common form being rotating. A change in direction means acceleration, since acceleration is change in motion (remember the example of going around in a circle from position, velocity, acceleration). Again, Newton's First Law is invalid for a rotating frame, or frame that is constantly changing orientation. Thus, Newton's First Law must only be valid for reference frames that are still or moving at constant velocity. This is a CRUCIAL concept to understand and when selecting reference frames, you ensure that you at least pick a correct one.

Newton's Second Law

In mathematical terms, $F_{net}=ma$. Note that both $F$ and $a$ are vectors, but $m$ is a scalar, so $F$ and $a$ have to be in the same direction (since multiplying by a scalar, in this case $m$, is not going to change the direction of the vector). $F_{net}$ is sometimes denoted as $\Sigma F$, the vector sum of all forces. The funny looking Greek character is the capital letter sigma, which essentially just means “sum”, or “net”.

It is important to realize that the net force results in the acceleration and never any other way around. Acceleration only comes by way of a net force. In that case, it may be more helpful to write the equation as $a=\frac{F_{net}}{m}$, which much more clearly implies the fact that acceleration is caused by a net force.

Now here's an entry level example of Newton's 2nd Law in action: If an object is moving at constant velocity, is there a net external force acting on it (Assume we are in an inertial reference frame unless mentioned otherwise)? Immediately, you should recognize that constant velociy means no acceleration. Therefore, if $a=0$, then $F_{net}=0$, by Newton's 2nd Law. This is another way to prove that force is not needed to maintain motion, nor does it directly cause motion, but rather, it changes motion. This will become more prevalent in the circular motion unit.

We typically won't do many complex calculations, albeit that we will use this knowledge to do some very basic, entry level problems. We will also be drawing free-body diagrams, because it is a super powerful tool, you will soon come to realize. Newton's Second Law is one of the hardest topics in mechanics to master, but its also one of the most important. You will probably be using this throughout the rest of the course, here and there. This just a preview, though. You will soon see the full power and might of Newton's 2nd Law when we talk about free-body diagrams. Newton's Second Law is actually one of the hardest parts of mechanic to fully master, because some of the problems involving such a simple little equation can get very, very complex and tough to work out. But don't worry too much about it. I believe you will be able to grasp it.

Newton's Third Law

Firstly, I would address the fact that Newton's Third Law is probably the most misunderstood, despite being one of the easiest laws to understand conceptually. How on Earth is this possible? Well, first, let me tell you what it actually means.

Essentially, if one object exerts a force on another it experiences an equal and oppositely directed force from the other object. It explains things such as recoil and makes rocket propulsion possible. Now, this may seem impossible and contradictory to experience. If all forces occur in equal pairs, wouldn’t motion be impossible?

However, there is one key thing to note about this law. The force pair does NOT act on the same object, but rather on different objects. And, according to the second law, acceleration of an object is proportional to both net force and mass. So, the two objects will have different accelerations assuming their masses are different, which reconciles this law with our observation and experience.

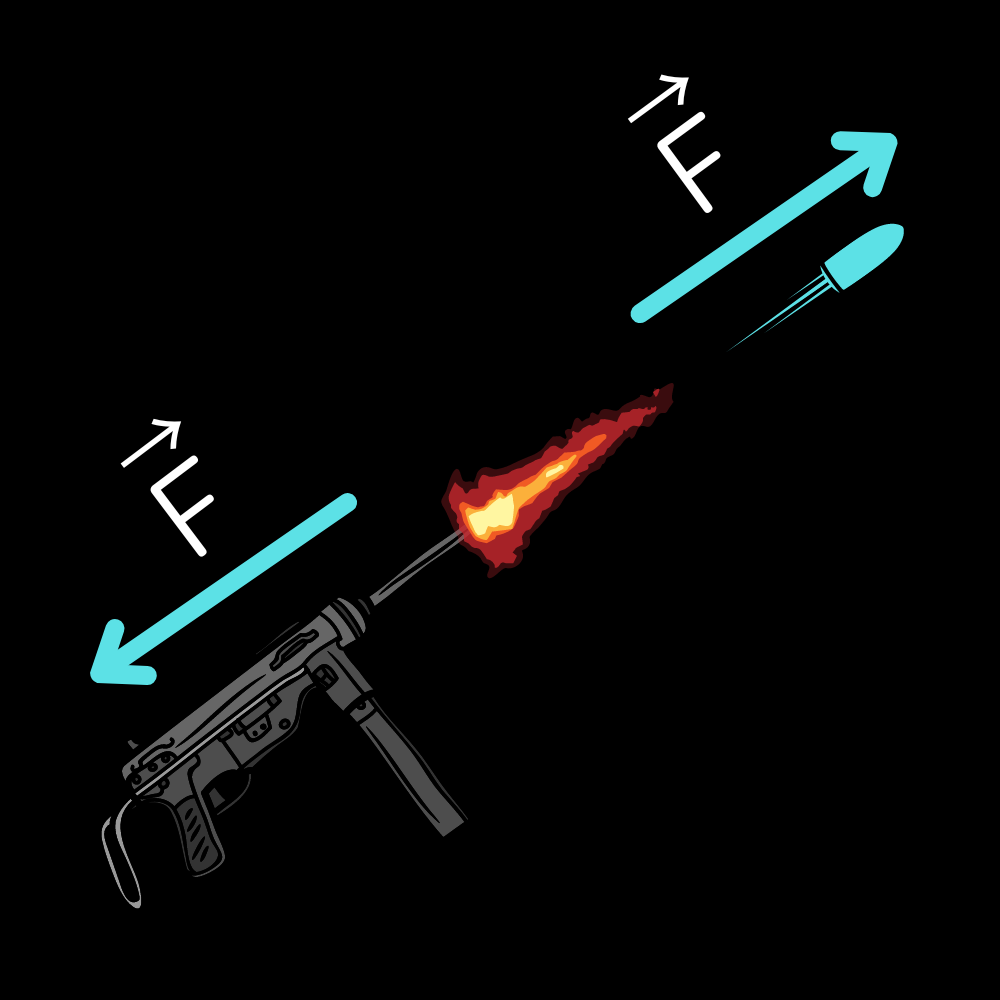
Let’s take a look at why Newton's Third Law is misunderstood sometimes. For example, say I asked you this question. What is the opposite and reaction force of the gravitational force the Earth exerts on you?

Maybe you would say it is the force that the ground exerts on you. However, this is actually incorrect. It is important to mention that Newton’s Third Law only applies to pairs of forces that belong to the same interaction. The interaction between you and Earth is completely different from the interaction between you and the ground. In actuality, the Newton’s Third Law equivalent for the force the ground exerts on you is the force you exert on the ground. Furthermore, you could have also reasoned that the two forces both act on the same object (you, the person), so they cannot be part of an action-reaction pair. An action-reaction force pair always acts on two different objects.

Thus, as crazy as it may sound, the Newton's Third Law pair for the gravitational force the Earth exerts on you is the gravitational force you exert on the Earth. (You will see why this is true in the lesson regarding Newton's Law of Gravitation.)

Conclusion

Surprisingly, Newton’s Third Law is not the most difficult to understand, it’s just that the way it is interpreted and presented often times is incorrect. Newton states "action" and "reaction", but in truth, there is no action and reaction. From now on, we will call these pairs "Third Law Pairs", because that's what they are. Finally, as an ending note, intuitively, you can think of it this way: Newton’s Third Law is like if I punch you in the face, I break my wrist, and not if I punch you, you punch me back.

But all these are just concepts. (Except maybe the Second Law.) Now let's put them to use with free-body diagrams!